Matemáticas chinas o inglesas

Esta semana ha saltado a la Internetidad (que sería algo así como la celebridad en Internet) que la sociedad británica de ciencias ofrecía una recompensa a los estudiantes ingleses que fueran capaces de resolver un problema de matemáticas procedente de los exámenes de acceso a la Universidad en China.

La intención era llamar la atención de que en algunas ramas de los estudios universitarios británicos el conocimiento de las matemáticas es paupérrimo.

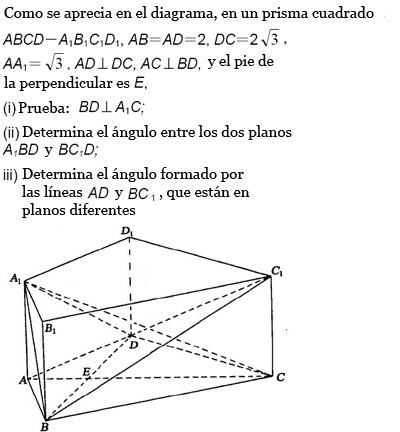
Junto con la noticia se podía encontrar una traducción del enunciado del problema:

Me ha llamado la atención la popularidad y la acogida que ha tenido el problema, pero también la incorrección de algunas de las soluciones propuestas. Es por esto que voy a intentar construir una demostración de las preguntas del problema mediante geometría métrica.

Para comenzar se debería fijar un sistema de coordenadas para poder referenciar todos los puntos, trazar vectores y realizar productos escalares. El origen de coordenadas se podría fijar en el punto D, y situar los puntos A, C y C₁ en los ejes X, Y y Z, respectivamente.

Asimismo, es claro que la figura es simétrica, ya que los lados AB y AD miden lo mismo y las diagonales son perpendiculares. Por tanto, BC = CD, y AB es perpendicular a BC.

Faltan por calcular los ángulos BAD y BCD, así como las longitudes de las diagonales AC y BD, y de los segmentos AE, EC, BE y ED.

Por el teorema de Pitágoras en el triángulo ABC se obtiene que la diagonal AC mide 4 unidades. Si se llama a al segmento AE, b al EC y 2b al BD (con lo que b = BE = ED) y con aplicación del teorema de Pitágoras:

• 4 = a² + c²
• 12 = b² + c²
• 4 = a + b

La resolución de este sistema de ecuaciones revela que a = 1, b = 3 y c = √3.

Los ángulos se pueden calcular con fórmulas trigonométricas básicas. Si se toma el triángulo DAE y se llama α al ángulo DAE, cos α = 1/2, por lo que α = 60º. Por tanto el ángulo DAB vale 120º, el EDC 60º, el ECD 30º y el BCD 60º.

Con esta información ya se pueden calcular las coordenadas del punto E. Si se supone que éstas son (a, b, 0), el producto escalar de los vectores DA y DE es el siguiente: (2, 0, 0) · (a, b, c) = |DA| · |DE| · cos 30º.

Por tanto, 2·a = 2 · √3 · √3 / 2, y a = 3/2. Utilizando la fórmula del módulo del vector DE y sabiendo el valor de a, b = √3 / 2. Aplicando este vector a D se obtiene el punto E, y aplicándolo de nuevo el punto B.

Ya se pueden situar todos los puntos de la figura: A = (2, 0, 0), B = (3, √3, 0), C = (0, 2·√3, 0), D = (0, 0, 0) y E = (3/2, √3/2, 0). Los puntos A₁, B₁, C₁, D₁ y E₁ son iguales pero con la tercera coordenada igual a √3.

Ahora la solución de las preguntas es trivial (en sentido amplio…):

1. Para ver que BD es perpendicular a A₁C es suficiente con realizar el producto escalar de los vectores: BD · A₁C = (-3, -√3, 0) · (-2, 2·√3, -√3) = 6 – 6 = 0. Como ninguno de los vectores es nulo el ángulo que forman es de 90º.
2. Para averiguar el ángulo que forman los planos A₁BD y BC₁D se debe calcular el ángulo que forman sus dos vectores normales.

   Los vectores normales de un plano se calculan mediante el producto vectorial de dos vectores no paralelos contenidos en él cualesquiera.

   Para el plano A₁BD se pueden escoger los vectores A₁B = (1, √3, -√3) y DB = (3, √3, 0), cuyo producto vectorial es (3, -3·√3, -2·√3).

   Para el plano BC₁D se pueden escoger los vectores BC₁ = (-3, √3, √3) y DC₁ = (0, 2·√3, √3), cuyo producto vectorial es (3, 3·√3, -6·√3).

   El producto escalar de ambos vectores normales es (3, -3·√3, -2·√3) · (3, 3·√3, -6·√3) = -9 -27 + 36 = 0. Es decir, el ángulo que forman los vectores normales y por tanto los dos planos es de 90º.

3. El ángulo entre las rectas AD y BC₁ es el ángulo que forman cualesquiera dos vectores contenidos en las rectas, como podrían ser DA = (2, 0, 0) y BC = (-3, √3, 0)

   Este ángulo se puede calcular con el producto escalar DA · BC = |DA| · |BC| · cos α. Es decir, -6 = 2 · 2 · √3 · cos α. Por tanto, cos α = √3/2, y α = 30º.

No es un problema difícil (de hecho una vez encontrados los ángulos y los lados es sencillo). Me atrevería a decir que es de un nivel menor que el esperado en la rama de ciencias de la selectividad española que hice yo en tiempos del BUP y el COU, aunque con una formulación algo diferente. Actualmente, por lo que me cuentan, puede tener una dificultad bastante alta.